Часть II. Начальные основы теории обучаемых систем управления

 

1. Теория образов в обучаемых системах управления

 

1.1. Рельефное представление образов.

 

Что такое образ? В простом человеческом понимании образом может быть фотография, картина или то, что мы видим, слышим, осязаем, то есть любая сложная информация. Всё это, вроде бы, понятно, но инженера такое толкование не устраивает, и не устраивает, по край­ней мере, по двум причинам: во-первых, в нём не определено понятие сложности, а во-вторых, не указана физическая форма информации.

Чтобы выйти на чисто инженерное определение образа, построим наши рассуждения так, чтобы постепенно уточнять физическую сторону образа. Для простоты возьмём техническую систему с очувствлением и выделим из всего рецепторного поля только сетчатку глаза; спрое­цируем на неё с помощью объектива изображение обозреваемой сцены и представим себе, что каждый её фоторецептор освещен по-своему. Это означает, что на выходе каждого из них будет своё электричес­кое напряжение, именуемое нами возбуждением. Фактическое распреде­ление рецепторных возбуждений по сетчатке глаза, очевидно, и есть рецепторный образ видимой сцены. Такое физически конкретное опреде­ление образа в частном случае — легко воспринимается, но всё-таки нуждается в дополнительном уточнении.

Что такое — фактическое распределение возбуждений? Выделим один какой-то рецептор сетчатки и определим его размерность. Так как он занимает вполне конкретное место на общем поле, то его положение может быть определено двумя координатами этого поля. А дополнив двумерное положение рецептора величиной его возбуждения, получим трёхмерную величину; такова размерность рецептора. Её — эту размер­ность — можно представить в виде вектора, перпендикулярного к полю очувствления, расположенного в конкретной точке этого поля и име­ющего длину, равную возбуждению. Если теперь представить таким об­разом все другие рецепторы, то вершины их векторов сформируют слож­ную кривую поверхность, напоминающую рельеф; этот рельеф даёт нам представление о фактическом распределении возбуждений рецепторов по всему полю. Он же является действительным рецепторным образом видимой сцены или, в общем случае, текущей ситуации.

Так мы определили образ. Остаётся только договориться о том, что удобнее представлять рецепторное поле плоским (это не искажает ин­формативность образа), а рельеф, — имеющим плоское основание.

Рельефные образы в оптических системах. Такими же рельефными можно считать образы в оптической обучаемой системе: и световой поток изображения, и диапозитивы, и даже распределение электричес­ких потенциалов по фотоэлектрическому экрану можно представить в виде рельефа. Начнём со светового потока изображения. Допустим, оптика собрала отражённые лучи обозреваемой сцены и направила их в виде светового потока с параллельными лучами по световому каналу оптической системы. Плотность светового потока по всему сечению канала окажется различной и будет соответствовать передаваемому тоновому изображению. Если мысленно пересечь световой поток пер­пендикулярной плоскостью и отложить от неё в каждой её точке по направлению света в виде векторов плотность светового потока, при­ходящегося на эту точку, то вершины векторов создадут рельеф, ко­торый можно рассматривать как образ обозреваемой сцены. Если же взять вместо мысленной секущей плоскости обычное матовое стекло и направить на него световой поток, то получим на нём видимое цвето­вое изображение, различная освещённость которого может быть воспри­нята как рельеф. Отсюда следует, что любую фотографию, как образ, можно представить в виде рельефа, если считать, что белый цвет на ней выступает над чёрным (для черно-белых фотографий).

Точно также в виде рельефа можно представлять диапозитивные образы, то есть фотопозитивы на прозрачной подложке, только в этом случае рельеф образует не белый свет, а прозрачность; такое изо­бражение можно назвать прозрачностным. Диапозитивы хороши тем, что позволяют оперировать с ними в сложных комбинациях различных обра­зов (чуть ниже мы это покажем); поэтому лучше даже видимую глазом сцену представлять также в виде диапозитива; при этом упрощаются преобразования светового потока в оптическом канале обучаемой сис­темы. Покажем это на примере, допустим, глаз обозревает какую-то сиену, освещенную рассеянным светом; оптика глаза собирает отра­жённый свет и направляет его в виде изображения по оптическому каналу. Это и есть действительный образ обозреваемой сцены. Точно такой же образ можно получить, используя диапозитив этой сцены: пропуская через него равномерный световой поток с параллельными лучами, получим на выходе такое же световое изображение; разницы в образах но будет, но второй случай более удобен для физического представления; изобразим его в следующих символах:

,

 

где U — равномерный световой поток с параллельными лучами; стрел­ка ( ® ) показывает направление потока света; A — диапози­тив обозреваемой сцены; B — световой поток с изображением на вы­ходе из диапозитива.

Эту же символику мы применим на последующих ступенях преобра­зования входного изображения в оптическом канале системы, а пока охарактеризуем U, A и B. Все они — образы, но у каждого есть своя особенность. Поток U можно представить в виде рельефа, самого простейшего по форме — как плоскогорье; это следует из того условия, что свет на входе принят равномерным по всему сечению по­тока. Он, благодаря такой своей особенности, проходя через диапо­зитив A, создаёт на выходе световой поток с изображением B, идентичным A. Поэтому можно считать, что B и A, как обра­зы, одинаковы; различие их — в том, что B — реальный световой поток, имеющий энергию и способный производить воздействие, до­пустим, на фотоэлектрический экран, в то время как A - пассив­ный образ, не располагающий энергией и не способный в чём-либо себя проявить.

Пропустим световой поток B через диапозитив мозга C и полу­чим на выходе сложный световой поток Д:

 

.

 

И С, и Д — тоже образы, но, опять же, C — пассивный образ, а Д — можно сказать, — активный. Парность таких образов, очевидно, является закономерностью: диапозитив работает только тогда, когда через него проходит свет.

Дальше в оптическом канале обучаемой системы поток Д попа­дает на фотоэлектрический экран; обозначим этот экран через F и будем считать, что он подобен диапозитиву, только на выходе у него не свет, а электричество. Как образ сам по себе, фотоэлектричес­кий экран F в нормальном состоянии представляют собой такой же простейший рельеф, как U, то есть плоскогорье; и только физические дефекты на нем способны исказить этот вид.

Образ F — пассивный, поэтому:

 

,

 

где G — распределение электрических потенциалов на фотоэлект­рическом экране, возникших под воздействием потока света Д;

G — последний образ в цепочке преобразований в оптическом ка­нале обучаемой системы; он также может быть представлен как рель­еф, но уже не оптический, а электрический.

За ним следует последняя операция — суммирование всех потенци­алов фотоэлектрического экрана; эта сумма и есть тот сигнал уп­равления E, который обучаемая система выдаёт на исполнительный привод; изобразим суммирование такой символикой:

 

.

 

Всю последовательность фотоэлектрических преобразований в оп­тическом канале обучаемой системы управления можно представить в виде следующей цепочки:

 

.              (2.1)

 

Символическая запись (2.1) отражает работу оптической системы, впрочем не только оптической, — такое же или почти такое образное представление может быть распространено и на электрические, и на гидравлические, и на любые иные системы.

Изобразим принятой символикой процесс обучения оптической сис­темы; он, как известно, сводится к итерационному видоизменению диапозитива мозга C. Пусть на очередном шаге обучения при предъ­явлении очередной j-ой ситуации (точнее: её диапозитива ) возникает фактический сигнал управления . Погрешность сиг­нала будет равна:

,

 

где  — требуемый сигнал в данной j-ой ситуации.

Далее следует такая процедура: при извлечённом диапозитиве мозга C направляют световое изображение ситуации  непосред­ственно на фотоэлектрический экран F и, регулируя диафрагму объектива, добиваются на выходе сигнала управления, равного по­грешности ; в символах образного представления получим:

 

,

 

где  — степень открытия диафрагмы объектива в очередной j-ой ситуации; эта степень является скалярной величиной и изменяется в пределах  . Сохраняя полученное положение диафрагмы, корректируют диапозитив мозга , сформулированный в предыдущей ситуации:

 

.

 

Символическая запись образа предыдущей проводимости с обратной скобкой  говорит о том, что корректирующий поток света  как бы застревает в диапозитиве , увеличивая его прозрачность до .

К сожалению, такой процесс, действительно, приводит лишь к на­ращиванию прозрачности диапозитива мозга, хотя нормальное обучение требует также и её уменьшения. Эта однонаправленность вынуждает прибегать к раздвоению общего светового потока на плюс- и на ми­нус-потоки, из которых первый формирует положительный сигнал уп­равления, а второй — отрицательный, но а результирующий сигнал определяется их разностью. Если погрешность сигнала управления  положительная, то наращивается прозрачность диапозитива мозга плюс-канала, а если — отрицательная, то — минус-канала.

До сих пор мы рассматривали цепочку чередующихся активных и пассивных образов: потоки света перемежались диапозитивами, — но в принципе это не обязательно. Потоки света могут складываться и вычитаться сами по себе, а диапозитивы могут собираться в пакет или дробиться на составные части. Примером наложения световых по­токов может быть соединение трёх разных цветных изображений на экране телевизора; можно объединить световые потоки от двух про­екторов, или использовать для этих целей призматическую оптику. Разделять световые потоки с оптическими изображениями сложнее, но и это можно делать с помощью, например, цветных светофильтров. Таким же путём можно дробить на части диапозитивы (имеются в виду составные части), а что касается собирания их в пакеты, то в этом нет никаких трудностей.

Собирание пассивных образов в пакет может быть условным; по­кажем это на примере последовательности фотоэлектрических преобразований (2.1), представив ее в следующем виде:

 

 

или даже так:

.

 

Арифметика и алгебра рельефных образов. Использованная симво­лическая запись отражает только физическую суть Фотоэлектричес­ких процессов к никак не определяет размерные отношения образов. Введём арифметику и алгебру образов, имея в виду при этом, что оперировать придется не числами, а рельефами; и сохраним принятие обозначения.

Пусть образы U, B и Д представляют собой рельеф световых потоков, образы A и C — рельефы прозрачностей диапозитивов, образ F — рельеф, своего рода, прозрачности фотоэлектрического экрана, преобразующей свет в электричество, а образ G — рельеф электрических потенциалов на экране. Уточним, что такое — проз­рачность диапозитивов. Представим диапозитив состоящим из абсолютно прозрачных и абсолютно непрозрачных точек; через прозрачные точки лучи света проникают без потерь, а на непрозрачных точках полностью исчезают. Следовательно, соотношение прошедшего через диапозитив светового потока и потока, падающего на него, опреде­лится соотношением количества прозрачных точек и общим их коли­чеством; последнее соотношение и есть прозрачность диапозитива; она может изменяться от нуля до единицы. У сложного диапозитива прозрачность по всему полю неодинаковая и может быть представлена, как мы условились, рельефом. Ограничение прозрачности единицей говорит о том, что диапозитив мотет только ослабить падающий на него поток света, но усилить его не может. Это условие нужно вос­принимать с оговоркой, что рассматриваемые нами диапозитивы явля­ются пассивными и не имеют своей энергии на усиление входного потока; в принципе же усиление возможно.

Определив прозрачность как степень пропускания света, устано­вим соотношение потоков до и после диапозитива: очевидно, поток света на выходе будет определяться произведением входного потока на прозрачность диапозитива; в рельефном представлении образов это выразится в перемножении соответствующих рельефов. Таким об­разом, последовательность фотоэлектрических преобразований (2.1) можно изобразить в виде системы следующих простых алгебраических выражений:

 

;

;                                            (2.2)

;

.

 

В системе (2.2) первые два выражения отражают перемножения рельефов оптических образов; третье выражение преобразует свет в электричество и  — тоже в такой же форме, а последнее выраже­ние отображает собирание или суммирование электрических потенци­алов фотоэлектрического экрана. Необычная форма записи, в которой знак суммирования S стоит после G, говорит о том, что про­исходит собирание рельефного образа с превращением его в скаляр­ную величину (если бы знак S стоял перед G, то мы должны были бы воспринять это как сумму рельефов). Физически суммирова­ние электрических потенциалов может быть осуществлено обычным сумматором на базе операционного усилителя. Кстати, оптический по­ток собирают, как известно, выпуклой линзой.

Перемножение рельефов, предложенное в системе выражений (2.2), нуждается в некотором уточнении. Прежде всего должны полностью совпадать контуры оснований перемножаемых рельефов. Под основанием рельефа светового потока будем понимать то сечение потока, кото­рое образуется условной перпендикулярной плоскостью, а за основа­ние рельефа прозрачности диапозитива примем плоскость самого диа­позитива. Другими словами, должно выдерживаться полное соответ­ствие расположения диапозитива относительно светового потока: не допустимы смещения, повороты или какое-либо несогласованное изме­нение масштабов рельефов.

Практически перемножение рельефов можно осуществить двумя спо­собами: физическим, путём натурного пропускания светового изображения через пакет перемножаемых диапозитивов, и расчётным, матричным — о нём разговор — далее; и в том, и в другом случаях полное соответствие рельефов обязательно.

Результат перемножения двух рельефов — тоже рельеф, но отлича­ющийся от сомножительных. Если в перемножении один из рельефов плоский, то он не изменяет форму своего сомножительного рельефа, а лишь пропорционально его увеличивает или уменьшает, то есть вы­ступает в качестве обычной скалярной величины. А единичный плос­кий рельеф вообще не изменяет свой сомножитель; поэтому при усло­вии, что рельефы U и F являются единичными, рельеф A можно приравнять к рельефу B, а рельеф Д — к рельефу G.

Перемножать можно не только рельефные образы разной модальности, то есть активные с пассивными, но и одной —, например рельефы прозрачностей двух и более диапозитивов между собой. Так резуль­тирующий рельеф пакета (AC) определится как произведение рель­ефов A и C, а, перемножив рельефы образов A, C и F, получим рельеф (ACF):

.

 

В результате система выражений (2.2) примет вид:

 

;

.

 

Такой переход через результирующий сомножитель называется кон­катенацией.

Если составление диапозитивов в пакет на языке арифметики озна­чает перемножение их рельефов, то удаление из пакета отдельного диапозитива нужно рассматривать, очевидно, как деление рельефа пакета на рельеф удалённого диапозитива, так что:

 

.

 

Интересно отметить, что при перемножении рельефов диапозитивов их выпуклость (кривизна) будет уменьшаться, а при делении, наоборот, — увеличиваться. В самом деле, в пакет можно набрать столько диапозитивов, что их результирующая прозрачность может оказаться близкой к нулевой; а удаляя диапозитивы, мы будем просветлять пакет.

Из четырёх арифметических действий над рельефами мы рассмотрели только два: умножение и деление, — рассмотрим остальные — сложение и вычитание. Складывать можно, как уже отмечалось выше, световые потоки, например разноцветные для получения цветного изображения, а вычитать можно из того же общего цветного отдельные монохрома­тические. В последнем случае вычитание физически сведется к разде­лению цветного изображения на составляющие монохроматические. В оптической обучаемой системе такое разделение может потребоваться в том случае, если будут использованы фотоэлектрические экраны с избирательной по длинам световых волн чувствительностью.

Сложение и вычитание рельефов никаких особых условий не требу­ют, кроме, опять же, строгого совпадения оснований, и не имеют, пожалуй, никаких ограничений, если не возражать против возможного перехода в обратный рельеф. Что это такое? Обратным рельефом, на­пример, по отношению к штампу является отштампованная деталь, по отношению к позитиву — негатив. Получается он путём вычитания за­данного рельефа из так называемого плоского нулевого. В оптической обучаемой системе он может потребоваться в случае применения фото­электрического экрана обратной полярности, то есть с постоянным электростатическим зарядом, который устраняется светом. Тогда, преж­де чем направить световой поток Д на экран, его нужно превратить в обратный; символика перехода в обратный рельеф образа Д такова:

.

 

Если же переход в обратный рельеф нереализуем или недопустим, то нужно иметь в виду, что при вычитании рельефы могут упереться в своё нулевое положение, которое является для них предельным. Предельное положение может возникнуть и при сложении, когда макси­мальный уровень рельефа упрётся в свой потолок. Такое явление ха­рактерно не только для арифметики рельефов: предельность, как ог­раничение изменения параметров, в технике хорошо известна, и с нею научились считаться. Регулируемое электрическое напряжение может увеличиваться только до своего наибольшего значения, определяемого потенциалом источника питания, а давление гидросистемы может изме­няться до давления настройки предохранительного клапана сверху и до атмосферного давления снизу, — и в этом нет ничего неожиданного, хотя линейное математическое моделирование чувствует себя в этих случаях неуютно.

Рельефные образы в электрических системах. О рельефном представ­лении очувствления электрических обучаемых систем уже упоминалось; рассмотрим теперь с этих позиций прохождение информационных пото­ков по всей системе. Начнём с того же очувствления. Рецепторное поле в нашем представлении — плоскость, на которой в определённом порядке расположены рецепторы. Этим полем может быть сетчатка гла­за с фоторецепторами. В каждой конкретной ситуации рецепторы испы­тывают определённое внешнее воздействие; рисунок этого воздействия по всему рецепторному полю может быть каким угодно сложным; это — образ A; представим его в виде рельефа с основанием в форме са­мого рецепторного поля.

Считаем, что все рецепторы по своей физической природе явля­ются резисторами и нуждаются в электрическом питании. Можно было бы взять для них единый источник питания, создающий одинаковое напряжение на всех рецепторах, и тогда образ этого питания пред­ставлял бы собой плоский рельеф. На самом деле всё рецепторное поле разбито на несколько рецепторных участков, и каждый участок имеет своё напряжение питания; следовательно, рельеф образа пи­тающего напряжения — обозначим его через  U — выглядит в виде ступенчатого рельефа. Накладывая образ  U  на образ A, получим образ B:

.

 

Он характеризует возбуждения рецепторов; о нём уже говорилось — он представляет собой также рельеф. Уточним его размерность. В электрических цепях принято согласовывать между собой напряжение и ток через сопротивление; но можно согласовывать потенциалы (те же напряжения) в разных точках через проводимость элемента, стоящего между ними. Сделать это можно в том случае, если в элек­трической цепи, кроме указанного элемента, есть ещё резисторная нагрузка, превосходящая сопротивление элемента. В электрических обучаемых системах такая нагрузка есть: она замыкает столбцовые шины мозга на другой полюс источника питания (на массу). Очевидно, электрическое напряжение на выходе рецепторного резистора может изменяться в зависимости от его проводимости в пределах: от вели­чины наибольшего напряжения источника питания до нуля; если про­водимость рецепторного резистора окажется равной единице, то есть наибольшей, то напряжения до него и после него окажутся одинако­выми; если же проводимость рецепторного резистора будет равна нулю, то напряжение на выходе рецептора окажется также равным нулю. Получается так, что возбуждение рецептора, то есть тот физический параметр, который возникает у него на выходе, есть то же самое электрическое напряжение, измеряемое в вольтах. Следовательно, проводимость рецепторов, формирующая образ A — величина безразмерная, не изменяющая размерность силового параметра (в нашем слу­чав — напряжения), воздействующего на них. В смысле размерности рецепторы подобны диапозитивам оптических систем: проводимость идентична прозрачности.

За рельефом B следует рельеф C, как образ проводимостей синапсов, выходящих на отдельную столбцовую пару мозга и через неё на отдельный исполнительный орган. На самом деле рельеф C не один; их столько, сколько всего столбцовых пар. Следовательно, рельеф B одновременно должен воздействовать на них всех (можно было бы в связи с этим спросить: а хватит ли мощности на это у него? — но оставим пока этот вопрос без ответа); происходит как бы разветвление рельефных последовательностей на несколько ветвей, но, так как они все подобны, рассмотрим сначала только одну из них.

Рельеф B, воздействуя на рельеф C, породит рельеф Д:

 

.

 

Последний представляет собой образ рецепторных долей сигнала управления. Размерность Д можно сохранить такой же, как у рель­ефа B, то есть как напряжение в вольтах, но, может быть, удоб­нее представлять её как электрический ток в амперах; и то, и дру­гое допустимо в рамках электрических законов; пусть будет второе. Тогда, собирая (суммируя) все токи рецепторных долей, получим сигнал управления E:

.

 

На этом последовательность рельефных преобразований заканчи­вается; в собранном виде она представляется такой:

 

.                          (2.3)

 

Как мы видим, она очень похожа на последовательность (2.2), но короче её на один шаг. Здесь, как и там, не отражена столбцовая парность мозга, делящая каналы на плюсовые и минусовые, но она подразумевается.

С учётом разветвления последовательности (2.3) на все испол­нительные органы получим:

 

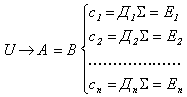.                           (2.4)

 

Ещё раз расшифруем смысловое значение входящих в (2.4) обозна­чений:

U — образ электрического питания, распределённого по всему рецепторному полю;

A — образ внешнего воздействия на рецепторное поле или, что одно и то же, образ проводимости этого поля;

B — образ возбуждения рецепторного поля;

, , ...,  — образы синаптических проводимостей различ­ных столбцовых пар мозга;

 , , ...,  — образы рецепторных составляющих (долей) сигналов управления различных исполнительных органов;

, , ...,   — сигналы управления отдельных исполнительных органов.

Из всех величин выражения (2.4) только сигналы управления E являются; скалярными, а остальные представляют собой рельефы. Однако, если рассматривать сигналы управления как единое целое и учитывать, что каждый из них действует на своём конкретном месте, то можно их семейство представлять тоже как образ и тоже как рельеф. Такой подход позволяет свести последовательность (2.4) к виду (2.3), но при этом трёхмерные рельефы  C и Д мы должны воспринимать уже как четырёхмерные, что несомненно услож­нит наше понимание процессов.

Символическая запись (2.3) отражает работу электрической обу­чаемой системы управления, но с помощью этих же символов можно показать также процесс обучения. Рассмотрим один из методов обу­чения, наиболее привлекательный по своему виду, — обучение подтал­киванием. Суть его заключается в том, что обучатель (человек-опе­ратор), подталкивая объект, например робот, в нужном направлении, воздействует на регуляторы (силарезисторы) дополнительного пита­ния отдельных столбцовых шин мозга, вызывая увеличение проводимос­тей синапсов, связанных с этими шинами. Он, очевидно, будет воздей­ствовать рефлекторно с таким усилием и так долго, пока не добьётся от объекта желаемых действий. Такой процесс обучения протекает непрерывно, но мы его рассмотрим в дискретной форме.

Прежде чем подталкивать объект в очередной  j-ой ситуации, обучатель, очевидно, должен выявить сначала его фактические дей­ствия, а если говорить только об одном исполнительном органе, то — его действительную скорость или, иными словами, его сигнал управ­ления. Преобразования определятся последовательностью (2.3):

 

,

 

где  — образ проводимостей синапсов, сложившийся в предыду­щей (j-1)-ой ситуации;  и  — фактические образ рецепторных долей и скаляр сигнала управления.

Имея в виду желаемые действия объекта , и сравнивая их с фактическими  , обучатель определяет погрешность сигнала управления :

 

.

 

В действительности он будет поступать сугубо рефлекторно, под­талкивая объект с нужной стороны, но величина такого подталкива­ния будет явно пропорциональна указанной погрешности. С другой стороны усилие подталкивания (или ) определит величину до­полнительного столбцового напряжения питания:

 

,

 

где  — коэффициент согласования.

Так как величины  и  — скалярные, то и  — скаляр, но для того, чтобы им можно было воздействовать в качестве актив­ного образа на пассивный рельеф , его следует превратить также в рельеф. Превращение скаляра в рельеф — процедура неслож­ная, но при условии, что последний должен быть плоским. (В прин­ципе скаляр можно превратить и в сложный рельеф, но для этого нужно задавать правила перехода в аналитической форме или в виде программы.) Дополнительное напряжение , в форме плоского рель­ефа вызовет изменение образа проводимостей синапсов , сфор­мированного в предыдущей ситуации, на величину , представляющую собой также рельеф:

 

.

 

Символическое изображение образа проводимостей синапсов со скобкой , как уже говорилось, означает, что активное воз­действие образа дополнительного возбуждения  уходит всё на изменение образа .

Результирующий рельефный образ проводимостей синапсов  оп­ределится пакетом рельефов  и :

 

.

 

При точной корректировке (при правильном подталкивании) изме­нение проводимостей синапсов на величину  должно привести к изменению сигнала управления на величину :

 

 

или, что одно и то же, к сформированию на выходе требуемого сиг­нала управления  после изменения проводимостей синапсов до величины :

.

 

В следующей ситуации процесс обучения с корректировкой образа проводимостей синапсов будет повторяться. Постепенно по мере ус­воения объектом тех навыков, которым его учили, подталкивания, очевидно, будут ослабевать и, наконец, прекратятся совсем, когда действия объекта устроят обучателя полностью.

Рельефность образов в выражениях (2.3) и (2.4) позволяет зримо представить изменение в поведении объекта при так называемом пе­реключении внимания системы управления, когда перераспределяется напряжение питания по рецепторным участкам. Такое перераспреде­ление, очевидно, изменяет форму рельефа образа U, а он уже изменяет всю последовательность дальнейших преобразований. В одной и той же ситуации A при одном распределении напряжения питания  сигнал управления будет одним:

 

,

 

а при другом распределении   — будет вторым:

 

.

 

Как видно из этих преобразований, достаточно изменить только один образ — образ питающего напряжения, и можно получить на вы­ходе системы иной сигнал управления, величина которого опреде­лится обучением.

Из рассмотренных преобразований рельефных образов, отражающих процесс обучения, не ясно, почему дополнительное напряжение   изменяет образ проводимости С, а основное напряжение U — не изменяет. Такое возможно, очевидно, только при условии, что образы U  и  имеют различную физическую форму; одна из них способна изменять проводимость синапсов, а другая — нет. В электрохимическом синапсе, например, постоянное питание U представляет собой гармонический электрический ток с симметричной амплитудой и определённой частотой — такой ток не способен вызывать электро­лиз, а дополнительное корректирующее питание  — тот же ток с той же частотой, но однонаправленный, со срезанной амплитудой — он порождает электролиз. Хотя эти токи в общем-то складываются (или вычитаются), но на схемах рельефных преобразований лучше этого не делать, чтобы не вызывать сомнения в нормальности процесса обучения.

Система алгебраических выражений, отражающая работу электричес­кой системы и её обучение подталкиванием (или вождением за руку) в образной форме имеет следующий вид:

· образные действия:

;

;

 

· переход от образа к скаляру:

 

;

 

· скалярное действие:

 

;

 

· переход от скаляра к образу в форме плоского рельефа:

 

;

 

· образное действие:

 

;

 

· умножение образа на скаляр:

 

,

 

где  — коэффициент согласования изменения проводимости синапса с дополнительным возбуждением рецептора;

· образное действие:

 

.

 

Завершают систему контрольные операции:

· образное действие:

 

;

 

· переход от образа к скаляру:

 

.

 

Те же действия в режиме конкатенации будут выглядеть так:

 

;

;

;

;

;

.

 

Скобками обозначены рельефные образы, полученные в результате перемножения рельефов и скаляров, входящих в конкатенационные пакеты.

Матричное (табличное) представление образов. Рельефы удобны для воображаемого представления (чтобы разобраться, например, в том, как трансформируется видимая сцена в сигнал управления) и даже иногда для оперирования ими (с помощью световых потоков изображе­ний и диапозитивов можно определять отношения образов), но не удоб­ны для вычислений. Вообще-то в электрических системах рельеф не является первородным: он составляется условно из возбуждений отдельных рецепторов, — и проще было бы в них оперировать трехмерными величинами самих рецепторов, но сложность состоит в том, что очень трудно (точнее, трудоёмко) определять местоположение каждого из них. Даже в сетчатке глаза, не говоря уж о другом очувствлении, с плотно уложенными фоторецепторами, когда их общее количество измеряется тысячами, а может быть даже — сотнями  тысяч, практи­чески невозможно проследить за каждым рецептором в отдельности: сколько же нужно иметь контролируемых выходов для этого? и как проследить, с какой точкой сетчатки связан каждый их них? И вызы­вает в связи с этим удивление, как решает эту задачу Природа, со­единяя вместе в мозгу нейроны, идущие от фоторецепторов, расположенных в конкретных местах сетчаток обоих глаз. Для чего это дела­ется — нам понятно: для согласованного сведения глаз, — но как это делается — нейрофизиологам неизвестно; а ведь в человеческом гла­зу, по крайней мере, — миллион выходов. И всё-таки разбираться в этом рано или поздно придется.

А пока можно пойти на некоторое упрощение — оно касается именно расположения рецепторов: расположим их строго геометрически, напри­мер в соответствии с прямоугольной сеткой, составленной из прямых строк и столбцов; такое расположение называется матричным или таб­личным. Оно позволяет заменить координаты точек номерами строк и столбцов; эти номера лишь отчасти указывают на местоположение рецеп­тора, а могут быть вообще не связаны с этим. Но упрощение при этом очевидно.

Итак, считаем, что все рецепторы уложены в виде матрицы, и каж­дый из них характеризуется тремя величинами (размерность, как ви­дим, сохраняется): номером строки расположения  j, номером столбца i и возбуждением b. И пусть принятая матричность распро­страняется по всей системе в неизменном виде, так что и подвод пи­тания к конкретному рецептору, и внешнее воздействие на него, и синапс, связанный с ним, и его рецепторная доля сигнала управления имеют те же номера строки и столбца, какие имеет он. Отсюда сле­дует, что размерности матриц по всей системе одинаковы. Осталось только договориться, что матрицы должны быть квадратными, с рав­ными числами строк и столбцов; такая форма, будем считать, ближе всего в общем случае к любому рецепторному полю; впрочем, квадратность — не обязательна.

Переход от рельефного рецепторного образа к матричному не столь уж радикальный, — рельеф в принципе остаётся, только основание его вместо параметрического стало признаковым (номер строки или стол­бца не есть параметр, а — признак, так как может обозначаться не только цифрами, но и буквами, символами и любым другим признако­вым способом).

Сложнее обстоит дело с переходом к матрично-табличному виду рельефных оптических образов, которые по природе своей не дискретны и нуждаются в условном дроблении. Возьмём, например, прямоуголь­ный диапозитив; для того, чтобы представить его состоящим из пря­моугольных кусочков, необходимо разделить его поле на определён­ное количество горизонтальных и вертикальных полос; и диапозитив тогда предстанет собранным из этих кусочков. Прозрачность в пре­делах каждого кусочка при тоновом изображении диапозитива не будет постоянной, но её можно считать неизменной с некоторой долей по­грешности. Разумеется, чем мельче размеры кусочков, тем эта пог­решность будет меньше. Каждый такой условный кусочек диапозитива может быть охарактеризован, как к рецептор, тремя величинами: но­мером строки (горизонтальной полосы), номером столбца (вертикаль­ной полосы) и усреднённой прозрачностью.

Если дробить по такому же правилу рельеф образа того же диа­позитива, то в результате он распадётся на отдельные столбики, вы­сота которых будет отражать прозрачность соответствующего участка диапозитива; назовем такой столбик пикселем. Усреднённая прозрачность каждого пикселя выразится в том, что его вершина (макушка столбика) будет плоской; и рельеф, собранный из пикселей, будет на­поминать окультуренные террасами холмы.

Матричное (табличное) представление образов в оптических системах может быть распространено, как и в электрических, на все фотоэлект­рические преобразования от входа до выхода системы; только при этом следует строго соблюдать соответствие пикселей на разных переходах. Если в электрических системах сквозная нумерация прослеживается по ходу отдельной рецепторной электрической цепи, то в оптических ка­налах такой опорной линии нет, и нужно каждый раз отталкиваться от краев изображений или от оптически выделенных элементов изображений.

Вычисления, ради которых рельефные образа заменены нами на мат­ричные, могут производиться теперь в виде операций над числами, при­чём вычисления могут выполняться фронтально в табличной форме с по­степенным переходом от одного образа к другому или одиночным сквоз­ным путём пиксельных (рецепторных) цепочек. Начнём со второго спо­соба.

Представим пиксели всех образов оптической обучаемой системы управления в виде основного параметра с нумерацией строк и столбцов рас­положения в матрице:

 — световой поток пикселя j-ой строки и i-го столбца образа U;

 — прозрачность соответствующего пикселя образа A;

 — световой поток соответствующего пикселя образа B;

 — прозрачность соответствующего пикселя образа С;

 — световой поток соответствующего пикселя образа Д;

 — коэффициент превращения света в электрический потенциал соответствующего пикселя образа  F;

 — электрический потенциал соответствующего пикселя образа G. Последовательность преобразований соответствующих пикселей в виде отдельной цепочки в оптическом канале системы в соответствии с (2.1) примет вид

 

.

 

Электрический потенциал  есть пиксельная доля сигнала управ­ления (ранее мы называли её рецепторной); сумма потенциалов всех пикселей образует сам сигнал управления:

 

,

 

где m — общее количество пикселей.

Изобразим последовательность преобразований пикселей в алгебра­ической форме в соответствии с выражениями (2.2):

 

;

;

;

.

 

При принятых условиях усреднённости основных параметров пикселей (плоская макушка столбиков рельефов) полученные выражения представ­ляют собой обычные арифметические действия над обычными числами.

Объединяя их воедино, получим:

 

.

 

Все промежуточные образы можно восстановить по пикселям этих об­разов, собирая их вместе в виде матриц.

Последовательность пиксельных преобразований в электрических сис­темах (напомним: пиксель соответствует в них рецептору) в принципе такая же, только вместо оптических операций в них происходят элект­рические, и содержание пикселей в них, соответственно другое:

 — напряжение питания рецептора  j-ой строки и i-го столбца;

 — внешнее воздействие на тот же рецептор;

 — возбуждение (напряжение на выходе) того же рецептора;

 — проводимость соответствующего синапса;

 — доля сигнала управления обозначенного рецептора.

Формально алгебраические выражения последовательности преобра­зований сохранятся такими же, что и у оптической системы, только переход через , а объединённое выражение примет вид

 

.                              (2.5)

 

Фронтальный метод расчета выполняете поэтапно согласно перехо­дам преобразований от образа к образу. Первый переход: ; матрицы образов U и A имеют вид

 

;   .

 

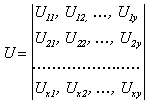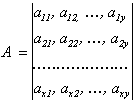Перемножение этих матриц сводится к перемножению пикселей, соответствующих друг другу по расположению, например ; , и так далее.

В результате получим матрицу образа B:

 

.

 

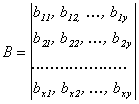И так далее от образа к образу.

Следует иметь в виду, что рассматриваемые здесь перемножения не имеют ничего общего с перемножением матриц в том разделе математики, который именуется матричным исчислением. В этом смысле наше матрич­ное представление образов можно было бы назвать просто табличным.

Пикселирование образов или рецепторно-табличное представление информации позволяет прийти к известному выражению (1.2), принятому нами за математическую модель работы обучаемой системы управления.

Заменим в выражении (2.5) произведение  на соответствующее возбуждение  и получим

 

,

 

где m — ещё раз напомним: общее количество рецепторов-пикселей.

Полученное выражение напоминает (1.2) и отличается от него толь­ко тем, что рецепторы-пиксели имеют двойную индексацию, определяю­щую их расположение в информационном канале.

Матричное (табличное) и, тем более, рельефное представление об­разов позволяет, прежде всего, упростить понимание обучаемых систем управления. Если в логических системах законы управления задаются решающими правилами, передаточными функциями или алгоритмами пере­ключений, то в обучаемых системах они выглядят как сложные образы (рельефы), формируемые в результате многократного наложения образов ситуаций друг на друга. Каждый в отдельности рецептор есть часть образа и как элемент образа принимает участие в формировании общего сигнала управления, и каждый синапс — тоже самое, и делают это они наравне со всеми; поэтому, чем больше рецепторов в системе очувствления, тем богаче образ и тем лучше управление; и порча отдельных из них не сильно исказит образ и также мало скажется на сигнале управления.

Кроме того оперирование рельефами позволяет определять численные отношения образов и выявлять влияние этих отношений на процесс обу­чения.

Но самым главным моментом в рельефно-образном представлении ин­формации является, пожалуй, то, что оно способствует выработке у человека (не у технических систем, а у человека, занимающегося этими системами) образного мышления, так необходимого и при системном анализе, и при принятии решений по законам нечёткой логики.

 

 

1.2. Профильное представление образов

 

Рельефный образ ситуации в прямоугольной системе координат трёх­мерен и поэтому не очень удобен для математических операций с ним. Образ можно упростить, если воспользоваться таким важнейшим прин­ципом обучаемых систем управления, как независимость информацион­ных каналов. Именно эта независимость позволяет определять отдель­ный сигнал управления системы как обычную алгебраическую сумму про­изведений возбуждении рецепторов на проводимости соответствующих синапсов. А в обычной алгебраической сумме, как известно, слагаемые располагаются в ряд и могут меняться местами (вспомним школьное правило: от перемены мест слагаемых сумма не меняется). Таким обра­зом, рецепторное поле можно представить в виде рецепторного ряда, то есть рецепторы можно расположить в одну цепочку вдоль некоторой номерной оси, а их возбуждения — перпендикулярно к этой оси; и тогда кривая, огибающая возбуждения рецепторов, будет выглядеть уже как профиль. В результате нам уда­лось рельефный образ ситуации заменить на равноценный ему про­фильный, имеющий только две координаты в прямоугольной системе координат: расположение на оси или номер i и возбуждение b.

Профильный образ ситуации может быть представлен огибающей кривой или, что значительно проще, цепочной чисел, каждое из которых является возбуждением определённого рецептора. Такое представление, как последовательный ряд возбуждений рецепторов, примем окончательно за образ ситуации, так что j-ю ситуацию можно изобразить в виде

 

, , ..., , ..., ,

 

где  b — возбуждение рецептора; индексы  1, 2, ..., i,..., m — номера рецепторов; всего рецепторов m.

Отметим некоторые свойства образа ситуации:

· образ есть последовательность чисел, отражающих возбуждения рецепторов;

· количество чисел образа может быть каким угодно, но не менее двух: ; одно число — число, два числа — уже образ;

· каждое число (каждый рецептор) имеет свой номер; номера чисел не должны совпадать;

· расположение чисел в образе (нумерация чисел) — произволь­ное; числа в образе можно переставлять, убирать или дополнять, но делать это можно только до начала обучения;

· числа образа (возбуждения рецепторов) могут быть только положительными.

Образ, у которого все числа равны единице, является особым образом с особыми свойствами; назовем его единичным.

Если рассматривать всё рецепторное поле в целом, то можно вы­делить на нём характерные участки, которые можно назвать элемен­тами образа. Рассмотрим эти элементы на примере сетчатки глаза: элементами зрительного образа являются пятна, границы или контуры пятен, линии, точки и полутоновые участки. Пятно есть участок рецепторного поля с равными возбуждениями рецепторов, причём при смещении изображения в любую сторону на величину не более, чем на один рецептор, возбуждения рецепторов сохраняются неизменными. Пятна можно характеризовать как яркие, тёмные или серые. Граница пятна или контур включает только те рецепторы, возбуждение которых изменяется при смещении изображения на один рецептор. Линия есть тот же контур, но без пятна; при смещении изображения поперёк линии на один рецептор возбуждения всех рецепторов изменяются. Точка охватывает только один или несколько компактно расположен­ных рецепторов, и при смещении изображения в любом направлении на величину одного рецептора возбуждения их изменяются. Полутоно­вые участии характерны тем, что рецепторы их хотя и слабо, но изменяют свои возбуждения при любом смещении изображения; полу­тоновой участок можно представить как широкую линию или большую точку.

Параметры образов. Параметры образов делятся на параметры, характеризующие отдельные образы, и на параметры, характеризую­щие соотношения двух и более образов. К первым относятся:

· сумма возбуждений рецепторов:

 

;                                         (2.6)

 

· сумма квадратов возбуждений рецепторов:

 

;                                      (2.7)

 

· удельное возбуждение i-го рецептора:

 

;                               (2.8)

 

· отношение суммы возбуждений  к сумме квадратов возбуждений :

.                                  (2.9)

 

К первой группе параметров относится также сигнал управле­ния , определяемый в соответствии с (1.2) как сумма произ­ведений возбуждений рецепторов на проводимости соответствующих синапсов. Этот параметр можно рассматривать и как определяющий соотношение двух образов, если за первый образ принять возбуж­дения рецепторов, а за второй — проводимости соответствующих синапсов.

Другие параметры характеризуют соотношения образов и выявля­ются в ходе теоретического обучения. К ним относятся:

· сумма произведений возбуждении однономерных рецепторов двух образов, например A и B:

 

;                            (2.10)

 

· отношение суммы произведений возбуждений однономерных ре­цепторов двух образов A и B к сумме квадратов возбуждений рецепторов одного из этих образов, например A:

 

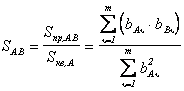.                   (2.11)

 

По своему смыслу данное отношение характеризует переход от образа A к образу B, поэтому назовем его коэффициентом приведения образа A к образу B;

· отношение квадрата суммы произведений возбуждений одноно­мерных рецепторов двух образов, например A и B, к произве­дению сумм квадратов возбуждений рецепторов этих образов:

 

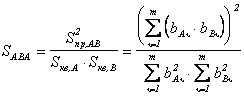.                 (2.12)

 

Это отношение по смыслу характеризует сходство двух образов, поэтому договоримся называть его степенью сходства двух образов A и B. Степень сходства трёх и более образов выражается ана­логично (2.12); так для образов A, B, C будем иметь

 

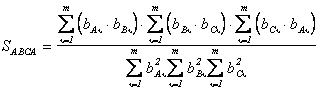.     (2.13)

 

Коэффициент приведения одного образа к другому. Прежде пояс­ним, почему отношение (2.11) мы назвали коэффициентом приведения. Для этого проведём краткое теоретическое обучение системы в со­ответствии с порядком обучения (1.12)...(1.16). Пусть первой си­туацией, в которой мы намерены провести обучение, будет ситуация A, отражённая образом возбуждений рецепторов: , , ..., ; и пусть требуемый сигнал управления в этой ситуации . Ис­ходное состояние системы — нулевое; это означает, что обобщённые проводимости всех синапсов рассматриваемой пары столбцов матрицы мозга равны нулю: . Поэтому до обучения фактический сиг­нал управления , определяемый выражением (1.12), окажется равным нулю:

.

 

Погрешность сигнала управления согласно (1.13) составит

 

.

 

В результате обучения поправка проводимости каждого i-го синапса, соответствующего j-му рецептору, определится согласно (1.15) как

,

 

а сами проводимости после обучения в ситуации A выразятся в соответствии с (1.16) в виде

 

.

 

На этом обучение в ситуации A завершается. И если после этого предъявить какую-то другую ситуацию, допустим ситуацию B с образом очувствления:  ,  , ..., , — фактический сигнал управления в ней определится согласно (1.12) как

 

.

 

А так как согласно (2.8) и (2.11)

 

,

 

то получим

 

.

 

Вывод таков: после обучения системы в первой ситуации факти­ческий сигнал управления в любой другой j-ой ситуации будет определяться коэффициентом приведения образа первой ситуации к образу j-ой ситуации:

 

.                                    (2.14)

 

Такая закономерность говорит о том, что название коэффициента  соответствует его сути, т.е. он приводит в соответствие сигналы управления в двух ситуациях. Важность коэффициента при­ведения одного образа к другому, определяемого формулой (2.14), подтверждается тем, что все теоретические исследования обучае­мых систем управления базируются на этих коэффициентах.

Из выражения (2.14) следует, что после обучения в первой ситу­ации A его (обучение) можно прекратить, если выполняется условие

 

,

 

или

 

,

 

где  — требуемый сигнал управления в любой j-ой ситуации;  — допустимое отклонение сигнала управления в этой ситуации.

В идеальном случае обучение завершается в первой A-ситуации и завершается без погрешностей, если

 

.

 

Рассмотрим некоторые свойства коэффициентов приведения; эти свойства вытекают из анализа выражения (2.11) и подтверждаются физическим содержанием; рассмотрим их по порядку.

1) Если договориться, что возбуждения рецепторов могут быть только положительными, то согласно (2.11) коэффициенты приведения будут также только положительными: . Это означает, что два набора возбуждений рецепторов соотносятся простыми поло­жительными числами, не переводящими один образ по отношению к другому в противоположное по знаку пространство.

2) В общем случае коэффициенты приведения могут иметь значе­ния от нуля и больше единицы: . Коэффициент приведения образа A к образу B будет равен нулю в том случае, если

 

,

 

а это физически означает то, что каждому значащему возбуждению рецептора одного образа соответствует нулевое возбуждение рецеп­тора другого образа, например:

образ A: 1 0 1 0 1 0 1 0 1 0;

образ B: 0 1 0 1 0 1 0 1 0 1.

Наиболее характерными значениями коэффициентов приведения являются значения, лежащие в пределах от нуля до единицы. Больше единицы коэффициент становится только тогда, когда второй образ более ярок, чем первый, т.е. в среднем во второй ситуации рецеп­торы возбуждены больше, чем в первой. При этом обратный (встреч­ный) коэффициент , отражающий приведение второго образа к первому будет, разумеется, меньше единицы. Если образы соизмеримы, то коэффициент приведения может оказаться равным единице, например, если

образ A: 5 4 3 2 1;

образ B: 4 5 3 2 2,

 

,

 

но обратный коэффициент  — коэффициент приведения образа B к образу A — будет иметь иное значение:

 

,

 

причём он в таких случаях никогда не может быть больше единицы.

 Из (2.11) следует, что  =1 также в том случае, если , т.е.

 

,

 

а такое возможно, в частности, при выровненных возбуждениях образа  и при = . Физическим примером рас­сматриваемого случая может быть сравнение изображений на сет­чатке глаза при изменении резкости изображения: образ A — при нулевой резкости, а образ B — при любой другой.

3) Прямой коэффициент приведения  в общем случае не равен обратному коэффициенту ; исключение составляют образы, у которых =  т.е.

 

,

 

и тогда =  и оба этих коэффициента не могут быть больше единицы.

4) Отношение прямого коэффициента приведения к обратному (встречному) равно отношению суммы квадратов возбуждений второго образа к сумме квадратов первого:

 

.

 

Отсюда следует, что отношение / больше единицы в том случае, когда >, а это означает, что образ B выгля­дит более контрастным, чем образ A.

5) Если образы A и B пропорциональны, т.е.  или , где k — коэффициент пропорциональности, то, подстав­лял это соотношение возбуждений в выражение (2.11), получим

 

,

 

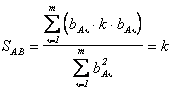а обратный коэффициент приведения определится как

 

.

 

Пропорциональные образы могут возникнуть в двух случаях: во­-первых, в одной и той же ситуации, но при разных напряжениях питания рецепторов, и, во-вторых, когда одна и та же обозреваемая сцена освещена в одной ситуации ярче, чем в другой. Таким образом, после обучения только в одной первой A-ситуации при предъявле­нии этой же ситуации, естественно, требуемый сигнал :  , но, если изменить напряжение питания в k раз или изменить освещение сцены во столько же раз, то сигнал управ­ления на выходе системы в этой измененной j-ой ситуации согласно (2.14) изменится во столько же раз: .

Если даже система обучена окончательно, на это ушло Т циклов обучения и в ситуации А фактический сигнал управления в соответствии с формулой (2.12) оказался равным

 

,

 

то в B-ситуации с пропорциональным образом сигнал управления определится как

 

.

 

Изменение сигнала на выходе системы при изменении напряжения питания рецепторов или при изменении освещённости сцены вовсе не говорит о том, что в целом поведение объекта будет другим; наоборот, пропорциональность сигналов управления в пропорциональ­ных ситуациях подтверждает неизменность поведения объекта — из­меняется лишь в той же пропорции скорости движения: и при повы­шении напряжения питания, и при усилении освещения сцены дей­ствия объекта станут лишь энергичнее.

6) Произведение прямого  и обратного  коэффициентов приведения двух образов даёт степень сходства этих образов:

 

,

 

7) Коэффициент приведения любого «нормального» образа к еди­ничному, у которого все возбуждения рецепторов равны единице: =1, — равен отношению суммы возбуждений «нормального» образа к сумме квадратов тех же возбуждений:

 

,

 

и чем контрастней образ А, тем меньше коэффициент приведения.

Стало быть, коэффициент приведения любого образа к единичному характеризует не отношение образов, а сам приводимый образ. Встречный коэффициент приведения единичного образа к любому об­разу А есть среднее арифметическое возбуждение рецепторов образа А:

 

.

 

Степень сходства образов. Сначала рассмотрим степень сходства двух образов, и для примера возьмём образы A и B с такими десятью возбуждениями:

образ А: 1 1 1 1 1 1 1 1 1 1;

образ B: 1 0 0 0 0 0 0 0 0 0.

Степень сходства этих образов, вычисляемая по формуле (2.12), определится как

 

,

 

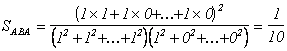т.е. при совпадении только одного возбуждения из десяти степень сходства образов равна одной десятой : = 0,1.

Увеличим число совпадающих возбуждений рецепторов до двух из десяти и получим степень сходства образов A и B равной двум де­сятым: = 0,2. Если же увеличить число совпадающих возбуж­дений до девяти:

образ А: 1 1 1 1 1 1 1 1 1 1;

образ B:1 1 1 1 1 1 1 1 1 0,

 то степень сходства образов A и B увеличится до 0,9.

Примеры о двоичными (1;0) возбуждениями очень наглядно харак­теризуют тот параметр сравнения образов, который определяется выражением (2.12) и который нами справедливо был назван степенью сходства двух образов. В случае с размерными возбуждениями со­держание рассматриваемого параметра не изменяется если размер­ные возбуждения представить ступенчатыми, то картина предстанет приблизительно такая же, как и о двоичными возбуждениями.

На основе пустого анализа выражения (2.12) можно получить некоторые свойства степени сходства образов.

1) Степень сходства двух образов равна произведению прямого и обратного (встречного) коэффициентов приведения:

Другими словами: степень сходства двух образов есть приведе­ние одного образа к самому себе через другой образ, причём пере­мена мест образов не изменяет степень сходства:

 

.

 

2) Степень сходства, как явствует из выражения (2.12), не мо­жет быть меньше нуля и больше единицы: ; при = 0 образы абсолютно различны, например:

образ А: 1 0 1 0 1 0 1 0 1 0;

образ B: 0 1 0 1 0 1 0 1 0 1,

а при = 1 — образы абсолютно схожи, т.е. ничем не отличаются.

Нетрудно предположить, что, чем меньше степень сходства об­разов ситуаций, тем быстрее будет происходить обучение системы, и, наоборот, чем больше степень сходства, тем труднее обучение. В пределе, когда степень сходства образов ситуаций равна единице, но в этих ситуациях требуются различные сигналы управления, то обучение и теоретически, и практически не возможно: такие ситу­ации назовем противоречивыми. Действительно, нельзя требовать от системы различных действий в одних и тех же ситуациях.

3) Интересно отношение степени сходства к образам, состоящим всего из одного числа. Пусть образ A — представлен одним числом  а образ B — числом  и пусть эти числа не равны между собой.

Вычисляя степень сходства таких образов по формуле (2.12), получим

 

.

 

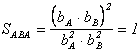Это значит, что обучаемые системы управления не различают подобные образы, или, другими словами, обучаемые системы не признают отдельное число за образ; образ для них возникает только тогда, когда он содержит не менее двух чисел, когда на практике система очувствления включает, по крайней мере, не менее двух рецепторов.

Интересно и то, что верхнего предела количества рецепторов у обучаемых систем управления нет. По этому поводу уместно напом­нить, что общее количество рецепторов у человека насчитывает больше 100 миллионов, и каких-либо затруднений в связи с этим человек не испытывает, скорее — наоборот: трудности возникают у него тогда, когда сокращается количество рецепторов.

4) Не менее интересно отношение степени сходства к пропор­циональным образам, которые упоминались при рассмотрении коэф­фициентов приведения и которые характеризуются соотношением , где k — коэффициент пропорциональности. Коэффи­циенты приведения таких образов равны: , . Следовательно, степень сходства пропорциональных образов, опре­деляемая как произведение коэффициентов приведения будет равна единице: . Эти образы, как ока­зывается, обучаемые системы управления также не различают.

Такое отношение обучаемых систем к пропорциональным образам на первый взгляд кажется загадкой: действительно, как можно не различать такие, например, образы:

образ А: 2 4 1 3;

образ B: 4 8 2 6?

Тем не менее — это так: обучаемые системы их не различают, так как = 1.

Эту загадку можно воспринять как должное, если вспомнить, что животные и человек пропорциональные образы также не различают. Каждый человек очень легко может убедиться в этом сам. Что такое — пропорциональный образ? Это — образ, в котором все возбуждения пропорционально изменены, например увеличены в два раза, как в рассмотренном выше числовом примере. На практике это означает, например, изменение освещённости обозреваемой сцены. И разве человек при этом по иному воспринимает видимое? Нисколько. Следовательно, восприятие пропорциональных образов роднит обучаемые системы управления с нервными системами животных и человека.

К слову, компьютеры, оснащенные техническим зрением и пред­назначенные для распознавания образов, очень чувствительны к изменению освещённости обозреваемой сцены. Они не способны воспринимать пропорциональные образы как одинаковые и нуждаются в дополнительных решающих правилах для того, чтобы правильно распознавать их.

5) Степень сходства трёх и более образов определяется как произведение всех коэффициентов приведения, включая замыкаю­щий коэффициент приведения последнего образа к первому:

 

.            (2.15)

 

И в этом случае, какими бы ни были по величине коэффициенты приведения, степень сходства будет лежать в пределах .

В заключение следует оказать, что соотношение образов, опре­деляемое степенью их сходства, выражается простым числом и поэтому очень удобно для пользования им в обучении и изучении обучаемых систем управления.

 

 

1.3 Определение коэффищентов приведения образов

 

Знание численных значений коэффициентов приведения образов ситуаций обучаемой выборки необходимо или желательно по многим соображениям. На основании соотношения коэффициентов приведения образов можно оценить ситуации, подобранные в обучаемую выборку, и при необходимости пересмотреть саму выборку, исключая из неё схожие ситуации и включая наиболее различимые. С помощью коэффи­циентов приведения можно выбрать наилучшую с точки зрения про­должительности обучения очерёдность предъявления ситуаций и тем самым значительно сократить время обучения и затраты на обуче­ние. В общем случае коэффициенты приведения образов позволяют оценить очувствление в целом, определить его возможности и пре­дела и выбрать усиление сигналов на выходе системы управления. В случае необходимости очувствление может быть изменено или дополнено, и снова в качестве оценочных параметров можно исполь­зовать коэффициенты приведения образов.

Особо следует выделить необходимость определения коэффици­ентов приведения в случае стандартизации оценок очувствления и в целом — обучаемых систем управления. В принципе достаточно предъявить две специально подобранные стандартные ситуации и определить численные значения коэффициентов приведения образов этих ситуаций, чтобы по ним дать оценку всей системе.

Расчётное определение коэффициентов приведения образов. Расчётным путём коэффициенты приведения можно определить лишь в том случае, когда есть возможность замерить возбуждения всех рецепторов. Для этого должны быть отсоединены все технические органы чувств от технического мозга и произведены замеры напряжений (или тока) на выходах всех рецепторов при подсое­динении их к определённой постоянной омической нагрузке в срав­ниваемых ситуациях. Не составляет особого труда расчетное опре­деление коэффициентов приведения образов в компьютерных обуча­емых системах управления с цифровой видеоаппаратурой в качестве технического зрения и со считыванием цифровых показаний с дру­гих органов чувств.

Напомним, что коэффициент приведения  образа А к образу B определяется по формуле (2.10), т.е. как отношение суммы произведений возбуждений однономерных рецепторов обоих образов  к сумме квадратов возбуждений первого образа А; встречный коэффициент приведения  образа B к образу А есть отношение той же суммы произведений  к сумме квадратов возбуждений уже второго образа B:

 

,       .

 

В свою очередь сумма произведений возбуждений двух образов   определяется по формуле (2.10), а сумма квадратов возбуждений  или  — по формуле (2.7) . При большом количестве рецепторов (тысячи, десятки тысяч и даже сотни тысяч) расчётное вычисление может превратиться в трудоёмкую операцию; осложняется работа ещё и тем, что при вычислении сумм произведений возбуждений парных образов необходимо строго соблюдать соответствие номеров рецепторов; так, например, возбуждение какого-то 12345-го рецептора в одной ситуации можно перемножить только о возбуждением того же 12345-го рецептора в другой ситуации. Сбиться о требуемого номера ре­цептора при большом их количестве очень легко, а результат при этом может оказаться совершенно негодным. Без использования компьютерной техники при вычислении коэффициентов приведения, оче­видно, не обойтись.

Экспериментальное определение коэффициентов приведения опти­ческих образов. Для обоснования экспериментального определения коэффициентов приведения оптических образов воспользуемся их рельефным представлением. Обратимся ещё раз к следующему выражению фотоэлектрических преобразований образов в —оптической системе:

 

.

 

В скобках представлен пакет диапозитивов (АС), один из которых А — обозреваемая сцена (образ оптической ситуации), а другой С —образ оптического мозга. На выходе системы — сигнал управ­ления , определяемый этими двумя образами. Тот же сигнал уп­равления  в той же ситуации в пиксельной (рецепторной) форме определится как

 

.

 

Заменим в выражении преобразований образов диапозитив А на А1 а диапозитив С на А2, получим:

 

.

 

В пиксельной форме этот сигнал управления  изобразится как

 

.

 

А теперь говорим, что образы А1 и А2 — это диапозитивы двух оптических ситуаций; следовательно,  есть просто сумма произ­ведений возбуждении однономерных пикселей в ситуациях А1 и А2.

Продолжим подстановки диапозитивов в разной их комбинации: установим в пакет два одинаковых диапозитива А1; преобразования образов примут вид:

 

.

 

или — в пиксельной форме:

 

.

 

Величину  можно охарактеризовать как сумму квадратов воз-буждений пикселей в ситуации А1.

 То же самое сделаем с диапозитивом А2:

 

;

.

 

Величина  представляет собой также сумму квадратов возбуж­дений пикселей, но уже в ситуации А2.

Произведённых подстановок диапозитивов достаточно для того, чтобы определить коэффициенты приведения образов ситуаций А1 и А2: прямой  и встречный , — а также степень сходства оптических образов этих ситуаций. По определению (2.11) коэффици­ент приведения одного образа к другому есть отношение суммы произ­ведений возбуждений однономерных пикселей обоих образов к сумме квадратов возбуждений пикселей первого образа. Следовательно, в нашем случае коэффициент приведения  образа ситуации А1 к образу ситуации А2 определится как

 

.

 

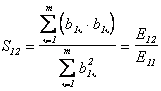Встречный коэффициент приведения  образа ситуации А2 к об­разу ситуации А1 по подобию можно определить следующим образом:

 

.

 

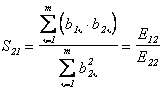Степень сходства образов этих оптических ситуаций в соответ­ствии с выражением (2.12) определится как

 

.

 

Полученные выражения позволяют определить коэффициенты приве­дения и степень сходства образов двух оптических ситуаций экспе­риментальным путём с использованием оптической обучаемой системы. Порядок выполнения работ следующий:

1) изготавливаем диапозитив А1 первой ситуации;

2) изготавливаем диапозитив А2 второй ситуации;

3) устанавливаем на оптическую обучаемую систему вместо диа­позитива мозга С диапозитив А1;

4) направляем оптическую обучаемую систему на сцену первой си­туации и определяем на выходе сигнал ;

5) направляем оптическую обучаемую систему на сцену второй си­туации и определяем на выходе сигнал ;

6) устанавливаем на оптическую обучаемую систему вместо диапо­зитива мозга С диапозитив А2;

7) направляем оптическую обучаемую систему на сцену первой си­туации и определяем на выходе сигнал ;

8) направляем оптическую обучаемую систему на сцену второй си­туации и определяем на выходе сигнал .

На этом эксперименты заканчиваются; проконтролировать точность экспериментов можно путём сравнения сигналов  и : они должны быть равны между собой; разность (-) отражает погреш­ность проведённых работ.

Коэффициент приведения  образа первой ситуации к образу вто­рой определится как отношение сигналов /; встречный коэф­фициент приведения  определится как отношение сигналов /, а степень сходства образов  этих двух ситуаций определится как отношение квадрата сигнала  к произведению сигналов  и  или как произведение полученных коэффициентов приведения:

 

.

 

При отсутствии специальных устройств оптических обучаемых сис­тем указанные эксперименты можно проводить с использованием под­ручных средств, например обычного диапроектора. Только в этом слу­чае нужно устанавливать в него не один диапозитив, а по два; оче­видно для этого нужно иметь дубли диапозитивов А1 и А2. Оценку величины светового потока на выходе из диапроектора можно производить с помощью фотоэкспонометра, который применяется в оп­тических системах для измерения освещённости. Можно использовать также обычный фоторезистор, направляя на него исходящий из диапроектора свет с помощью собирающей выпуклой линзы.

Выражение коэффициентов приведения через оптические образы по­зволяет уяснить физическую суть этих коэффициентов. Представим их условно в таком виде:

 

;

,

 

где скобками указаны пакеты диапозитивов.

Пакеты из спаренных дубль-диапозитивов (А1, А1) и (А2, А2) можно рассматривать почти как одиночные диапозитивы с повышенной контрастностью: их прозрачные места при наложении сохранятся почти такими же прозрачными, а тёмные — , накладываясь друг на друга, ста­нут ещё более тёмными; в результате проходящие через: пакеты этих дубль-диапозитивов потоки света  и  уменьшатся совсем незначительно.

Другое дело, когда спаренными окажутся разные диапозитивы (А1, А2); тут прозрачные места одного могут наложиться на тёмные места дру­гого и, наоборот, тёмные места первого — на прозрачные места второ­го ( так оно, собственно, и произойдёт, если диапозитивы действи­тельно окажутся различными). Указанное перекрытие приведёт к умень­шении результирующей прозрачности пакета диапозитивов и к уменьше­нию проходящего через него потока света; и, очевидно, чем больше будет несхожесть оптических образов диапозитивов А1 и А2, тем меньшей окажется их парная прозрачность и тем слабее будет поток света , проходящий через них.

А так как этот поток света  в представленных выше выражениях для определения коэффициентов приведения располагается в числи­теле, то, очевидно, именно он будет определять их величины: чем больше окажутся несхожими по расположению светлых и тёмных пятен диапозитивы двух разных оптических ситуаций, тем меньшим окажется числитель.

Таков общий вывод; но он не охватывает все варианты необычного сочетания диапозитивов. Рассмотрим, в частности, один такой случай. Пусть диапозитив А1 будет очень прозрачным по всему своему полю, а диапозитив А2, наоборот, — затемнённым. Общая прозрачность пакета (А1, А2) будет близка прозрачности одного диапозитива А2, прозрачность пакета (А1, А1) будет близка прозрачности диапозити­ва А1, то есть сохранится большой, а прозрачность пакета (А2, А2) окажется, очевидно, близкой нулю. Такое сочетание даст следующий результат:

 

;

.

 

Но, что касается степени сходства  образов этих диапозитивов, то она, как уже говорилось, в любом случае не превышает единицу. Отвлекаясь от частных случаев отметим, что результирующая прозрачность пакета из двух различных диапозитивов будет определяться совпадением их светлых пятен и в том числе даже самых мелких, отражающих мелкие детали видимых сцен.

Экспериментальное определение, коэффициентов приведения образов с обнулением проводимостей синапсов. Следует ещё раз напомнить о том, что электрические обучаемые системы управления работают не с внешней информацией (не с внешними параметрами), а с внутренней, т.е. о теми фактическими возбуждениями рецепторов, которые возникают в данной ситуации. Следовательно, коэффи­циенты приведения образов не могут быть определены на основе только ситуаций обучаемой выборки, они — коэффициенты — при­вязаны к конкретной обучаемой системе управления и могут быть определены исключительно по показаниям конкретных технических органов чувств этой системы. Поэтому возникает необходимость экспериментального, т.е. натурного, определения коэффициентов приведения образов.

Выберем сначала такие обучаемые системы, технический мозг которых способен обнуляться, т,е, проводимости синапсов могут не только наращиваться во время обучения, но и уменьшаться (стираться) до нуля для переобучения. В качестве сравниваемых образов примем образы ситуаций обучаемой выборки, количество которых вполне определенно.

В основу экспериментального определения коэффициентов при­ведения положим хорошо известную нам зависимость (2.14), сог­ласно которой после обучения системы только в первой ситуации, например в ситуации А, фактический сигнал управления  в любой другой  j-ой ситуации будет определяться коэффициентом приведения  образа первой А-ситуации к образу j-ой ситуации. Приведём выражение (2.14) к виду

 

,                                        (2.16)

 

где Е(А,А) — фактический сигнал управления в А-ситуации системы, обученной предварительно в этой же ситуации.

Порядок экспериментального определения коэффициентов приве­дения таков:

1) обнуляем технический мозг;

2) выбираем в качестве первой базовой ситуации ситуацию А и предъявляем её системе; замеряем фактический сигнал управ­ления Е(0,А) — он должен быть равен нулю; отклонение от нуля не должно превышать допустимого, выбранного нами заранее;

3) задаем требуемый сигнал ; он не должен быть очень малым, близким нулю — в противном случае деление на него в соответствии с выражением (2.16) было бы невозможным; обучаем систему; после обучения производим контрольную проверку: заме­ряем фактический сигнал управления Е(А,А) в той же А-ситуации — он не должен отличаться от требуемого сигнала  более чем на допустимое отклонение;

4) предъявляем по очереди вое прочие ситуации обучаемой выборки; в каждой из них замеряем фактический сигнал управления Е(А,j) и по формуле (2.16) рассчитываем коэффициент приведения  образа А-ситуации к образу соответствующей j-ситуации;

5) обнуляем технический мозг;

6) выбираем в качестве второй базовой любую ситуацию обу­чаемой выборки кроме А-ситуации, например В-ситуацию; повторяем операции 2), 3), 4) данного алгоритма и получаем коэффициенты приведения  образа В-ситуации к образам  прочих j-ситуаций;

7) эксперимент повторяем с поочередным выбором в качестве базовой всех прочих ситуаций обучаемой выборки.

Так можно определить все коэффициенты приведения образов, включая встречные, и общее число их определится как , где n — число ситуаций в обучаемой выборке.

Экспериментальное определение коэффициентов приведения образов в процессе непрерывного обучения. Предлагаемый способ определения коэффициентов приведения образов не требует обну­ления технического мозга. Прежде чем составить алгоритм (по­рядок) эксперимента, получим необходимые аналитические выра­жения. Вначале рассмотрим обучаемую выборку, состоящую всего из двух ситуаций А и В, в которых заданы сигналы управления соответственно  и . Для определения коэффициента при­ведения  мы можем воспользоваться формулой (2,16) и рас­смотренным выше порядком эксперимента, но для определения встречного коэффициента приведения  этого недостаточно.

Воспользуемся теоретическим обучением в двух ситуациях, выполненным ранее, и выпишем из него выражение для фактичес­кого сигнала управления Е(АВ,А) на 1-ом шаге 2-го цикла; оно выглядит так:

 

.

 

Из него можно получить:

 

.                               (2.17)

 

Выражения (2.16) и (2.17) позволяют определить оба — пря­мой и встречный — коэффициента приведения. Порядок эксперимента таков:

1) убеждаемся, что исходное состояние технического мозга — нулевое; для этого в обеих ситуациях А и В замеряем фак­тический сигнал управления на выходе системы — он должен равняться нулю с точностью допустимых отклонений  и ;

2) предъявляем ситуацию А; в качестве первой ситуации желательно выбрать такую из двух имеющихся, в которой требу­емый сигнал  не доложен быть равным нулю или близким к нему; проводим обучение; проверяем фактический сигнал управ­ления Е(А,А) в той же А-ситуации;

3) предъявляем ситуацию В; замеряем фактический сиг­нал управления Е(А,В), по формуле (2.16) вычисляем коэффициент ;

4) дообучаем в ситуации В; проверяем правильность обу­чения: замеряем фактический сигнал управления Е(АВ,В) и убеждаемся, что он равен сигналу ;

5) предъявляем ситуацию А  и замеряем фактический сиг­нал Е(АВ,В); по формуле (2.17) вычисляем коэффициент .

На этом определение коэффициентов приведения образов двух ситуаций завершено, но обучение может быть продолжено.

Рассмотрим теперь обучаемую выборку, состоящую из трёх ситуаций А, В, С с заданными сигналами управления соответст­венно , , . И снова для выведения необходимых формул обратимся к теоретическое обучению, проведённому ранее. На З-ем шаге 1-го цикла хода обучения в трёх ситуациях, т.е. при предъявлении С-ситуации, фактический сигнал управления был определён как

 

.

 

Из этого выражения можно получить

 

.                            (2.18)

 

Если после теоретического обучения на З-ем шаге 1-го цикла предъявить снова ситуацию А, то фактический сигнал управ­ления Е(АВС,А), очевидно, будет таким:

 

.

 

Откуда:

 

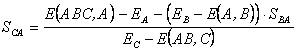.       (2.19)

 

Если же предъявить вместо ситуации А ситуацию В, то получим фактический сигнал управления Е(АВС,В):

 

.

 

Из этого выражения выведем формулу для определения :

 

.        (2.20)

 

После получения необходимых формул можно приступить к экспериментальному определению коэффициентов приведения (начало действий будет совпадать с первыми шагами предыду­щего алгоритма):

1) убеждаемся, что исходные проводимости технического мозга — нулевые;

2) предъявляем ситуацию А; проводим обучение;

3) предъявляем ситуацию В; замеряем фактический сигнал Е(А,В); по формуле (2.16) вычисляем коэффициент ;

4) предъявляем ситуацию С; замеряем фактический сигнал Е(А,С); по формуле (2.16) вычисляем коэффициент ;

5) предъявляем ситуацию В; дообучаем систему;

6) предъявляем ситуацию С; замеряем фактический сигнал управления Е(АВ,С); по формуле (2.18) вычисляем коэффициент ;

7) предъявляем снова ситуацию А; замеряем фактический сигнал Е(АВ,А); по формуле (2.17) вычисляем коэффициент ;

8) предъявляем ситуацию С; дообучаем систему;

9) предъявляем ситуацию А; замеряем фактический сигнал Е(АВС,А); по формуле (2.19) вычисляем коэффициент ;

10) предъявляем ситуацию В; замеряем фактический сигнал Е(АВС,В); по формуле (2.20) вычисляем коэффициент .

На этом экспериментальное определение коэффициентов приведения образов трёх ситуаций завершается. По аналогии могут быть определены коэффициенты приведения и в тех случаях, когда число ситуаций в обучаемой выборке окажется больше трёх.