3.4. Динамика смещающегося
образа
При смещении взора и при изменении положения объекта образ его очувствления видоизменяется. При плавном смещении изменение образа будет также плавным, а плавное изменение образа вызывает в общем случае плавное изменение сигналов управления. Этим можно объяснить округление острых углов пешеходных тропок: для живых существ указанное округление имеет силу закона.
Зависимость
изменения образа от величины смещения у различных образов различная, и
определяется она характером самого образа, а точнее — соотношением таких его элементов, как пятна, контуры,
полутоновые участки, линии и точки. Пусть из общего количества рецепторов m пятнами охвачены p рецепторов, контурами —
k рецепторов, а линиями и точками — ![]() рецепторов, так что
рецепторов, так что ![]() . Полутоновые участки с
плавно изменяющимися возбуждениями рецепторов причислим к контурам. И приведём
все смещения органов очувствления, имеющие различные размерности и масштабы, к
смещению возбуждений рецепторов рецепторного поля; проще говоря — к смещению образа. В этом случае за единицу
смещения можно принять сам рецептор. При смещении образа на x рецепторов (в общем случае —
без указания направления) контуры и полутоновые участки, очевидно, начнут
расширяться, охватывая всё большее количество рецепторов:
. Полутоновые участки с
плавно изменяющимися возбуждениями рецепторов причислим к контурам. И приведём
все смещения органов очувствления, имеющие различные размерности и масштабы, к
смещению возбуждений рецепторов рецепторного поля; проще говоря — к смещению образа. В этом случае за единицу
смещения можно принять сам рецептор. При смещении образа на x рецепторов (в общем случае —
без указания направления) контуры и полутоновые участки, очевидно, начнут
расширяться, охватывая всё большее количество рецепторов: ![]() , где
, где ![]() — коэффициент пропорциональности, отражающий
расположение рецепторов и направление перемещения образа, — а размеры пятен
будут соответственно уменьшаться:
— коэффициент пропорциональности, отражающий
расположение рецепторов и направление перемещения образа, — а размеры пятен
будут соответственно уменьшаться: ![]() . Останутся неизменными в количественном отношении только
линии и точки:
. Останутся неизменными в количественном отношении только
линии и точки: ![]() =
=![]() =const.
=const.
Динамику
образа будем оценивать по-прежнему с помощью коэффициента приведения этого
образа к самому себе при смещении его на x рецепторов, т.е. с
помощью коэффициента приведения предыдущего образа к последующему ![]() , и с помощью степени
сходства этих образов
, и с помощью степени
сходства этих образов ![]() . В общем виде
указанный коэффициент приведения будет таким:
. В общем виде
указанный коэффициент приведения будет таким:
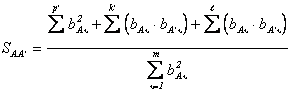 , (2.70)
, (2.70)
а степень сходства изобразится как
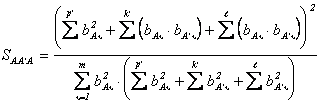 . (2.71)
. (2.71)
Начнём с
самого простого образа, представляющего собой одно сплошное пятно; тогда ![]() =0, k =0, p = m. Само собой разумеется,
что такой образ при смещении никак измениться не сможет, значит:
=0, k =0, p = m. Само собой разумеется,
что такой образ при смещении никак измениться не сможет, значит: ![]() =1;
=1; ![]() =1. Примером такого образа может быть зрительное поле в виде
равномерно освещенного фона.
=1. Примером такого образа может быть зрительное поле в виде
равномерно освещенного фона.
Усложним образ
и наложим на сплошное пятно линии и точки; рецепторы распределятся так: k =0; ![]() + p = m. При смещении
образа более чем на один рецептор в каждый момент времени изменять свои
возбуждения будут только рецепторы линий и точек, общее количество которых
будет всегда одно и то же:
+ p = m. При смещении
образа более чем на один рецептор в каждый момент времени изменять свои
возбуждения будут только рецепторы линий и точек, общее количество которых
будет всегда одно и то же: ![]() =
=![]() =const;
следовательно, выражения (2.70) и (2.711) в
данном случае будут иметь вид
=const;
следовательно, выражения (2.70) и (2.711) в
данном случае будут иметь вид
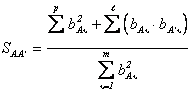 ;
;
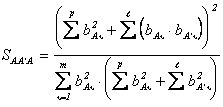 ,
,
а это значит, что и коэффициент
приведения ![]() , и степень сходства
, и степень сходства
![]() будут иметь
постоянные значения на всём диапазоне смещения независимо от величины
смещения, причем чем большее количество рецепторов будет охвачено линиями и точками,
тем больше коэффициент
будут иметь
постоянные значения на всём диапазоне смещения независимо от величины
смещения, причем чем большее количество рецепторов будет охвачено линиями и точками,
тем больше коэффициент ![]() и степень
и степень ![]() будут отклоняться от
единицы.
будут отклоняться от
единицы.
Общий случай,
когда в образе присутствуют все элементы, характерен тем, что коэффициент
приведения ![]() и степень сходства
и степень сходства
![]() сильно зависят от
величины смещения образа. Именно такому случаю соответствуют выражения (2.70) и (2.71).
сильно зависят от
величины смещения образа. Именно такому случаю соответствуют выражения (2.70) и (2.71).
|
Рис.2.8. Идеальный «шахматный» образ |
Более подробно
рассмотрим динамику образа, состоящего из
пятен (с контурами), но без линий и точек. Идеальным случаем возникновения
такого образа может быть обзор глазом шахматного поля, у которого абсолютно
белые квадратные по форме клетки перемещаются с такими же по форме абсолютно
чёрными клетками. Если иметь в виду, что рецепторы парны: на один рецептор
света приходится один рецептор темноты, — и предположить, что рецепторы имеют
идеальные рабочие характеристики, согласно которым освещенные рецепторы света
и затемнённые рецепторы темноты максимально возбуждены, а затемнённые рецепторы
света и освещенные рецепторы темноты имеют нулевые возбуждения, то получим идеальный «шахматный» образ (рис.2.8), у которого клеткам шахматного поля будут
соответствовать его пятна. Контуры пятен (границы клеток) при смещении образа
будут расширяться и всегда будут равны смещению образа x.
Рецепторы контуров при смещении образа будут менять свои возбуждения на обратные:
если прежде возбуждение какого-то рецептора было наибольшим, то, попадая в зону
контура, оно становится нулевым, и наоборот. Поэтому при смещении образа на
величину x в пределах от 0 до размера пятна а часть рецепторов, а именно: ![]() — поменяет свои
возбуждения на обратные.
— поменяет свои
возбуждения на обратные.
Коэффициент приведения исходного образа к последующему, смещенному определится как
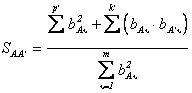 .
.
Произведение
возбуждении ![]() тех рецепторов, что
расположены в зоне контуров в силу опрокидывания возбуждений на обратные,
очевидно, всегда будет равно нулю, поэтому коэффициент приведения
тех рецепторов, что
расположены в зоне контуров в силу опрокидывания возбуждений на обратные,
очевидно, всегда будет равно нулю, поэтому коэффициент приведения ![]() будет иметь вид
будет иметь вид
 .
.
Если числом m обозначить общее
количество пар рецепторов и если по-прежнему считать, что в каждой паре один
рецептор возбужден максимально, а другой —
нулевой, то, определяя общее количество пар рецепторов, охваченных пятнами в
последующем образе как ![]() , получим выражение
для коэффициента приведения
, получим выражение
для коэффициента приведения ![]() , справедливое в интервале x = 0...2a:
, справедливое в интервале x = 0...2a:
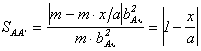 .
(2.72)
.
(2.72)
Встречный
коэффициент приведения ![]() определится как
определится как
 .
.
А так как
возбуждения каждой пары рецепторов в обоих сравниваемых образах одинаковы (они
лишь поменялись местами), то встречный коэффициент ![]() оказывается равным
прямому коэффициенту
оказывается равным
прямому коэффициенту ![]() :
:
![]() .
.
Степень сходства предыдущего и последующего образов определится в том же интервале x = 0...2a как
![]() .
(2.73)
.
(2.73)
|
Рис.2.9. Динамика смещающегося шахматного образа |
Зависимости
коэффициентов приведения ![]() ,
, ![]() (2.72) и степени сходства
(2.72) и степени сходства ![]() (2.73) от смещения
образа x представлены
на рис. 2.9. В исходном состоянии, когда x = 0 , и при смещении на x =2a
коэффициенты приведения
(2.73) от смещения
образа x представлены
на рис. 2.9. В исходном состоянии, когда x = 0 , и при смещении на x =2a
коэффициенты приведения ![]() ,
, ![]() и степень сходства
образов
и степень сходства
образов ![]() равны единице. При
увеличении смещения образа в интервале x = 0...a
коэффициенты приведения и степень сходства
уменьшаются вплоть до нуля при x = a,
а затем при дальнейшем смещении в интервале x = a...2a, снова возрастают
до единицы в положении x = 2a. Далее всё
повторяется.
равны единице. При
увеличении смещения образа в интервале x = 0...a
коэффициенты приведения и степень сходства
уменьшаются вплоть до нуля при x = a,
а затем при дальнейшем смещении в интервале x = a...2a, снова возрастают
до единицы в положении x = 2a. Далее всё
повторяется.
«Шахматный»
образ является сугубо искусственным, но он хорош тем, что позволяет оценивать
очувствление обучаемой системы управления; по этой причине к нему можно
прибегать для сравнения систем. Если обучить обучаемую систему только в
исходной ситуации А и получить в ней сигнал управления ![]() с допустимым отклонением
с допустимым отклонением
![]() , то при смещении
образа в ситуации
, то при смещении
образа в ситуации ![]() сигнал управления
согласно (2.14) должен быть равен
сигнал управления
согласно (2.14) должен быть равен ![]() .
.
|
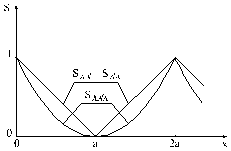
Рис.2.10. Сравнение
фактического |
На графике
(рис.2.10) полученный теоретический
сигнал управления ![]() повторяет зависимость
повторяет зависимость ![]() ; при нулевом смешении
x=0 сигнал управления равен
; при нулевом смешении
x=0 сигнал управления равен ![]() ; а при x = a он уменьшается до нуля.
; а при x = a он уменьшается до нуля.
Действительный
(фактический) сигнал управления ![]() при смещении «шахматного»
образа будет изменяться как-то иначе: у каждой системы он будет изменяться
по-своему.
при смещении «шахматного»
образа будет изменяться как-то иначе: у каждой системы он будет изменяться
по-своему.
Очевидно, чем
совершенней очувствление системы, тем ближе будет действительный сигнал управления ![]() к теоретическому
к теоретическому ![]() и тем меньше
будет разность между ними
и тем меньше
будет разность между ними ![]() , то есть погрешность. Эта погрешность, как видно из
графика, постоянно изменяется, но ее можно осреднить, если замерить площадь между
кривыми (заштрихованную площадь) и поделить её на смещение а:
, то есть погрешность. Эта погрешность, как видно из
графика, постоянно изменяется, но ее можно осреднить, если замерить площадь между
кривыми (заштрихованную площадь) и поделить её на смещение а:
![]() .
.
Таким образом,
по средней погрешности ![]() можно судить о
качестве очувствления обучаемой системы.
можно судить о
качестве очувствления обучаемой системы.
Из графика (рис.2.10)
можно определить также другие показатели, например точность позиционирования ![]() и темновой сигнал
управления
и темновой сигнал
управления ![]() . Точность
позиционирования или, точнее, нечувствительность системы определяется как
смещение образа на такую величину
. Точность
позиционирования или, точнее, нечувствительность системы определяется как
смещение образа на такую величину ![]() в окрестностях x=0 и
x = a, при
которой фактический сигнал управления изменяется на величину не больше
допустимого отклонения
в окрестностях x=0 и
x = a, при
которой фактический сигнал управления изменяется на величину не больше
допустимого отклонения ![]() . Темновой сигнал
управления
. Темновой сигнал
управления ![]() определяется как
тактический сигнал в позиции x = a, когда теоретический
сигнал
определяется как
тактический сигнал в позиции x = a, когда теоретический
сигнал ![]() равен, нулю.
равен, нулю.